graph LR
A[Model Compression] --> B[Pruning]
A --> C[Distillation]
A --> D[Quantization]
A --> E[PEFT]
B --> B1[Unstructured Pruning]
B --> B2[Structured Pruning]
B --> B3[Rank Reduction]
C --> C1[Logit Distillation]
C --> C2[Hidden-State Distillation]
D --> D1[Post Training Quantization]
D --> D2[Quantization Aware Training]
Model Compression for Efficient Training & Inference of Large Language Models
Laith Zumot • 2025
Practical Model Compression

Quantization
- Reduce precision of weights/activations to shrink memory & speed up math
- e.g., BF16 → FP8.
- Lower memory footprint → larger batch / context on same hardware
- Higher arithmetic intensity → faster GEMMs / attention
- Cheaper deployment on edge/CPU
- PTQ (Post-Training Quantization)
- No retraining; quick to try
- Needs calibration data to estimate activation ranges
- Schemes: per-tensor/per-channel, symmetric/asymmetric
- Gotchas: outliers, distribution shift, layerwise sensitivity
- QAT (Quantization-Aware Training)
- Best accuracy under low bit-widths (fake-quant + STE)
- Matches deploy time numerics (quant/dequant in-graph)
- Common formats & typical use
- FP8 (e4m3/e5m2): high throughput training/inference; mild loss
- INT8: robust sweet spot for prod inference
- MXFP4: used in GPT-OSS for MOE experts (MP).

Quantization — calibration, scaling & pitfalls
- Core knobs
- Granularity: per-channel (kernels) > per-tensor
- Ranges: min/max, percentile clipping, KL-based, EMA observers
- Rounding: nearest vs stochastic; smooth quant for activations
- Calibration goals
- Estimate activation/weight ranges that minimize clipping & rounding error
- Use representative samples (same domains/prompts/seq lengths as prod)
- Track both quality (e.g., perplexity, accuracy) and latency/memory
- Range estimation
- Min–Max / AbsMax (fast; risk of outlier blow-up)
- Percentile clipping (e.g., 99.9th) to tame long tails
- KL-divergence / MSE minimization to pick bins
- EMA observers during QAT for stable moving ranges
- Scaling schemes
- Symmetric (zero-point = 0): common for weights
- scale = max(|x|) / qmax - Asymmetric (nonzero zero-point): common for activations
- scale = (x_max − x_min) / (qmax − qmin) - Granularity: per-channel (weights) > per-tensor; group-wise for INT4
- Symmetric (zero-point = 0): common for weights
- Outlier management
- Keep sensitive parts in higher precision: embeddings, LM head, K/V proj
- SmoothQuant-style activation smoothing (shift dynamic range into weights)
- Weight-only quant (e.g., W8A16 / W4A16) to avoid activation quant error
- Implementation tips
- Static (ahead-of-time) quantization with calibration > dynamic on GPUs
- Fuse ops (conv/linear + bias + activation) before quantization if possible
- Align scales with kernel requirements (tile sizes, tensor cores)
- For QAT: fake-quant + STE; freeze observers late; fine-tune LR ↓
- Pitfalls & mitigations
- Distribution shift between calibration & prod → recalibrate by traffic slice
- Saturation in attention/LayerNorm paths → leave in FP16/FP32
- Dequant overhead on small layers → quantize hot GEMMs first
- INT4 regressions → use group-wise scales, try QAT/QLoRA, or back off to INT8
- Sequence length sensitivity → calibrate at prod seq lengths
- Validation checklist
- A/B: task metrics (↓ perplexity Δ, ↑ exact-match) + latency/throughput + VRAM
- Layerwise sensitivity sweep; opt-out layers that cause large drops
- Save scales/observers with model artifacts; log calibration dataset hash
Distillation
Train a student model to match a teacher model’s output distribution (soft targets).
Loss (with temperature \(T\)): \[ \mathcal{L} = (1-\alpha)\,\mathrm{CE}(y, p_s) \;+\; \alpha\,T^2\,\mathrm{KL}\!\left(p_t^{(T)} \,\|\, p_s^{(T)}\right) \]
Backprop only through the student; the teacher is frozen.
Variants: use KL or JS divergence; mix in hard-label CE; schedule \(T\) or label smoothing.
Online distill: teacher forward + student forward/backward (higher GPU but no disk I/O).
Offline distill: cache teacher logits; cheaper GPU at train time but larger storage/I/O.
Issues:
- Training cost: Expect ~20–30%+ extra memory for activations/gradients beyond raw parameter memory (depends on context length, batch size, kernels).
- Exact logit matching can be restrictive; the student may imitate outputs without learning richer internals.
- Students may not learn intermediate representations; consider feature/attention distillation or auxiliary losses.
- length/verbosity bias from the teacher; mitigated with CE mixing, calibration, and data augmentation.
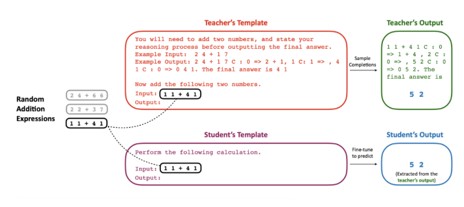
Post Training - Distilling 405B / 70B → 8B (Order-of-Magnitude)
- Memory Footprints (FP16/BF16, params only)
| Model | Params | Approx. Memory |
|---|---|---|
| Teacher (large) | 405B | ~810 GB |
| Student | 8B | ~16 GB |
- Activations & gradients: add ~20–30% overhead (implementation- and length-dependent).
- Teacher inference-only memory (online distill):
- 405B: ~1 TB+
- Student training memory (8B, long context ~128k): ~160 GB
- (model + activations/optimizer; depends on sharding/checkpointing).
- Hardware Sketches
- Teachers
- 405B:
- 16–24× H100 80GB, tensor/pipeline parallel
- InfiniBand interconnect
- ~2 TB system RAM
- 405B:
- Student (8B)
- 2× H100 with NVLink
- ≥256 GB RAM host
- Fits comfortably with mixed precision + gradient checkpointing
- Teachers
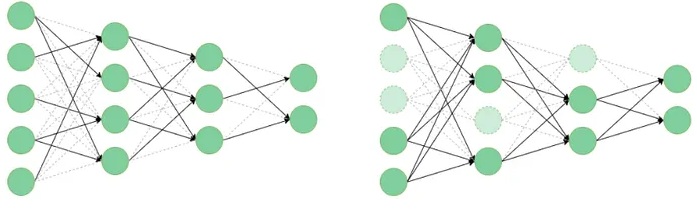
Pruning
Reduce params/FLOPs/VRAM; potential latency gains (esp. with sparse kernels).
How weights are pruned
- Unstructured (element-wise): highest sparsity; requires efficient sparse kernels
- Structured (channels/filters/heads): immediate speedups; lower flexibility
- N:M sparsity (e.g., 2:4): HW-friendly pattern; good accuracy/speed trade-off
Which weights to prune
- Magnitude-based (|w|, L1/L2): simple, strong baseline
- Movement pruning (|Δw| during fine-tune): preserves changing weights
- Gradient/Taylor saliency: |g·w| (first-order importance)
- SNIP/GRASP (pre-train sensitivity analysis);
- Optimal Brain Surgeon (2nd-order, costly)
- Head importance via contribution/entropy; prune low-value heads
- Magnitude-based (|w|, L1/L2): simple, strong baseline
Scheduling
- One-shot: prune once → (re)train (fast/risky)
- Iterative/gradual: increase sparsity over steps
- Example cubic schedule to target S*: S(t)=S*·(t/T)^3
Pruning — Strategies
- What counts as “prunable”?
- Global Rank weights across all layers → prune globally. Maximizes sparsity.
- Layerwise layer-specific thresholds to avoid over-pruning critical layers.
- How to fix accuracy post-pruning
- Retrain/Rewind: Fine-tune the pruned model; optionally revert to a pre-pruning checkpoint.
- Optionally add distillation style loss (logits or hidden states) to mimic the original model’s outputs/logits during retraining
- End-to-end workflow
- Establish baseline: task metrics, perplexity, latency/throughput, VRAM.
- Sensitivity sweep: per-layer sparsity curve (e.g., 0→90%) to find fragile blocks.
- Choose pattern: unstructured | structured (channels/heads) | N:M (e.g., 2:4).
- Set sparsity budget: global target + layerwise caps (protect embeddings/LN).
- Schedule: one-shot or gradual (e.g., cubic to S* over T steps).
- Prune & recover: brief fine-tune with small LR; consider distillation.
- Export & realize speed: use kernels that honor sparsity (structured / N:M).
- Validate in prod-like loads: seq length, batch size, mixed precision.
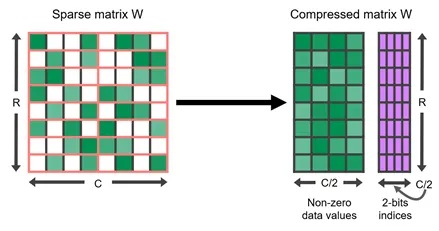
Pruning — Recovery
- Recovery training
- LR: 0.1–0.3× of fine-tune LR; no warmup or very short.
- Masking:
- Fixed-mask (recommended): Keep pruned weights at 0 permanently → deterministic deployment.
- Re-growth (Rigged Lottery): Allow new connections early, then freeze later.
- RigL dynamically re-grows pruned connections and prunes less important ones cyclically
- Inspired by the Lottery Ticket Hypothesis: It searches for high-performing sparse subnetworks by “rigging” the connectivity in favor of high-potential weights.
- Regularizers:
- L1-loss (unstructured): Encourages more zeros.
- Group Lasso (structured): Penalizes entire channels/groups
- Distillation (optional):
- add KL(logits) and/or feature loss to preserve behavior.
- Checkpoints:
- Rewind/Reset weights to a pre-prune checkpoint mid-recovery if unstable.
# Pseudocode for RigL_training
def RigL_training(model, sparsity_ratio, update_freq, total_steps):
initialize_sparse_mask(model, sparsity_ratio) # Random or pruned
for step in 1...total_steps:
train_one_batch(model) # Optimize active weights
if step % update_freq == 0 and step < 0.8 * total_steps:
prune_mask = bottom_k_weights(model, prune_ratio) # Smallest weights
regrow_mask = top_k_gradients(model, prune_ratio) # Pruned weights w/highest |∇L|
update_mask(model, prune_mask, regrow_mask) # Swap connectionsPruning — Caveats
- Structured pruning specifics
- Dimensions Matter:
- Prefer removing entire heads/MLP channels to get immediate kernel wins.
- Example: Removing only 2 attention heads reduces num_heads and subsequent projection sizes.
- Post-Surgery Calibration:
- Run 10–100 inference steps to recompute network statistics (e.g., LayerNorm means).
- Hardware Gains:
- Removing entire blocks unlocks native kernel optimizations (e.g., cuDNN group conv).
- Dimensions Matter:
- Caveats & gotchas
- Sparsity ≠ speed
- Unstructured sparsity benefits only with sparse accelerators (e.g., Ampere GPUs)
- Structured/N:M always wins for latency.
- Over-tokenized (Llama3) may have limited pruning headroom.
- Excessive attention-head pruning can harm long-context/generalization.
- Prune-then-quantize usually more stable than quantize-then-prune; if mixing, plan QAT.
- Do NOT prune embeddings/LayerNorm/residual dims
- For deploy speedups, match your HW: structured or N:M > random sparsity
- Typical safe starts: 30–50% structured OR 60–90% unstructured
- Sparsity ≠ speed
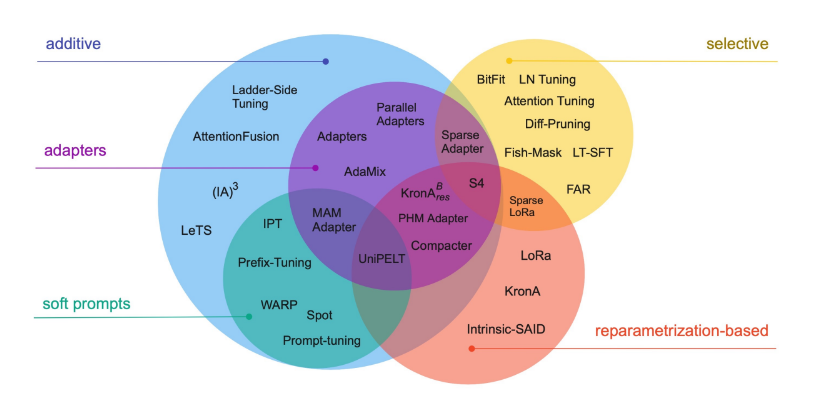
PEFT
- Parameter-Efficient Fine-Tuning = freeze the base model and train a small set of extra parameters (adapters, low-rank deltas, prompts).
- Tiny trainable footprint (often <1% of params) → fits on modest GPUs
- Faster training & lower memory/IO; checkpoints are small & swappable
- Multi-task: keep multiple adapter heads for different domains
- Core patterns
- Adapters: small bottleneck MLPs inserted in blocks
- LoRA/DoRA: learn low-rank (or decomposed) deltas on weight matrices
- Prefix/Prompt/Soft-prompt: learnable tokens prepended to inputs/keys
- IA³ / BitFit: learn per-feature scalars (attn/FFN) or just biases
LoRA Deep Dive — mechanics
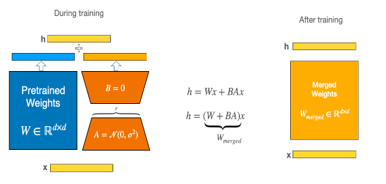
Freeze base model weights:
\[\begin{aligned} $W \in \mathbb{R}^{d_\text{out} \times d_\text{in}}$ \end{aligned}\]Learn low-rank weight delta:
\[\begin{aligned} W' &= W + \Delta W \\ \Delta W &= BA \\ \end{aligned}\] \[\begin{aligned} where: $A \in \mathbb{R}^{r \times d_\text{in}}$ , $B \in \mathbb{R}^{d_\text{out} \times r}$, $r \ll \min(d_\text{in}, d_\text{out})$ \end{aligned}\]Apply adaptive scaling:
Forward pass uses: \[Wx + \frac{\alpha}{r} B(Ax)\] (\(\alpha\) = tunable scaling constant)Optional regularization:
LoRA Dropout applied directly to input \(x\)
LoRA Deep Dive — sample code
# Pseudocode for LoRA
class LoRAparam(nn.Module):
def __init__(self, features_in, features_out, rank=1, alpha=1, device='cpu'):
super().__init__()
self.lora_A = nn.Parameter(torch.zeros((rank,features_out)).to(device))
self.lora_B = nn.Parameter(torch.zeros((features_in, rank)).to(device))
nn.init.normal_(self.lora_A, mean=0, std=1)
self.scale = alpha / rank
self.enabled = True
def forward(self, original_weights):
if self.enabled:
# Return W + (B*A)*scale
return original_weights + torch.matmul(self.lora_B, self.lora_A).view(original_weights.shape) * self.scale
else:
return original_weights
def linear_layer_parameterization(layer, device, rank=1, lora_alpha=1):
features_in, features_out = layer.weight.shape
return LoRAparam(features_in, features_out, rank=rank, alpha=lora_alpha, device=device)
nn.utils.parametrize.register_parametrization(net.linear1, "weight", linear_layer_parameterization(net.linear1, device))LoRA Deep Dive — configs
- Where to apply (LLMs)
- Attention: q_proj, k_proj, v_proj, o_proj
- MLP: up_proj / down_proj / gate_proj
- Key knobs
- rank r: 4–64 typical; higher r = more capacity/memory.
- lora_alpha: 8–64; acts like gain. Pair with r (e.g., r=16, α=32).
- lora_dropout: 0.0–0.1; helps regularize on small data.
- bias: usually “none”; keep base biases frozen.
- Training config (rules of thumb)
- Optimizer: AdamW (β=(0.9,0.999)), wd=0.0–0.1 (often 0 for LoRA).
- LR: 1e-4 to 5e-4 (instruction tuning) or 5e-5 to 2e-4 (task/classif).
- Warmup 3–5%; cosine or linear decay; grad clip 0.5–1.0.
- Mixed precision (BF16/FP16), gradient checkpointing for long seqs.
- Small KD logits loss can stabilize instruction-following.
- QLoRA (LoRA on 4-bit bases)
- Weight quantization: load base in 4-bit NF4 (normal float 4) with double quantization; compute in BF16/FP16.
- Train LoRA adapters in FP16/BF16; base remains frozen INT4 → huge VRAM savings.
- Use paged optimizers (e.g., paged AdamW) to avoid OOM with long contexts.
- Keep embeddings & output head at higher precision if quality dips.
- Typical config: r=16–64, α=32–64, dropout=0–0.05; target q,v,(o,up/down) first.
- Deployment
- Inference can merge (W) into (W) (for dense FP weights) or keep adapters separate (preferred with quantized bases).
- Export only adapter checkpoints for lightweight shipping.
Other PEFT Variants — Adapters, Prefix/Prompt, IA³, BitFit, DoRA
- Prefix / Prompt / P-Tuning v2
- Prompt-Tuning: Learns soft prompts (trainable embeddings) exclusively at the input layer.
- weaker performance on large domain shifts (Prompt-Tuning)
- Prefix-Tuning: Learns task-specific K/V vectors across multiple layers, offering higher capacity than Prompt-Tuning. -increased sequence length costs (Prefix-Tuning).
- Recipe: 20–100 virtual tokens; Prefix on deeper tasks, Prompt for light retargeting.
- Prompt-Tuning: Learns soft prompts (trainable embeddings) exclusively at the input layer.
- IA³ (Intrinsic SA Scalings)
- Learns feature-wise scaling vectors applied multiplicatively to weights in attention (Q,K,V) and FFN layers.
- Minimal parameters (<1% of base model) and near-zero latency overhead
- Recipe: enable scalars in attn proj & FFN gating; LR≈1–2e-4; wd=0.
- BitFit
- Train only biases.
- Pros: microscopic checkpoints; surprisingly strong when task ≈ pretrain.
- Cons: limited capacity on hard domain shifts.
- Recipe: unfreeze biases + LM head; LR≈1–3e-4; early stop.
- Adapters (Houlsby / Pfeiffer)
- Insert small bottleneck MLPs in blocks; train only adapter params.
- Houlsby, two adapters sequentially within one layer of the transformer, one after the multi-head attention and one after the FFN sub-layer, while
- Pfeiffer et al., adapter is inserted only after the FFN “add & layer norm” sub-layer.
- Recipe: insert after attention & MLP; b=32 start; LR≈1e-4; wd=0; warmup 3%. GELU activation, and near-identity initialization
- Insert small bottleneck MLPs in blocks; train only adapter params.
- DoRA (Decomposed LoRA)
- Decompose weight into magnitude × direction; learn low-rank updates to direction.
- Often more stable than vanilla LoRA, esp. with quantized bases.
- Recipe: replace LoRA with DoRA on sensitive mats (q,v); r=8–32, α=16–32.
- Choosing among them (quick cues)
- Tiny budget / many tasks → Prompt/Prefix, BitFit, IA³
- Need stability & modularity → Adapters
- Max perf/param → LoRA/DoRA (add QLoRA if VRAM-bound)
- Tiny budget / many tasks → Prompt/Prefix, BitFit, IA³
Example of LoRA FT
Citations & Further Reading
Citations & Further Reading
Images created w Gemeni
“Model Compression and Efficient Inference for Large Language Models: A Survey” https://arxiv.org/html/2402.09748v1
“Efficient Compressing and Tuning Methods for Large Language Models: A Systematic Literature Review” https://dl.acm.org/doi/10.1145/3728636
“Advances and Challenges in Large Model Compression” https://dl.acm.org/doi/fullHtml/10.1145/3675417.3675487
[Q1] ZeroQuant: Yao et al. 2022 https://arxiv.org/abs/2206.01861
[Q2] Outlier-Suppression: Wei et al. 2022 https://arxiv.org/abs/2209.13325
[Q3] Bondarenko et al. 2023 “Quantizable Transformers” https://arxiv.org/abs/2306.12929
[Q4] BinaryBERT: Bai et al. 2021 https://arxiv.org/abs/2109.12934
[D1] Step-by-Step Distillation: Hsieh et al. 2023 https://aclanthology.org/2023.findings-acl.432
[D2] GKD: Agarwal et al. 2023 https://arxiv.org/abs/2306.13649
[D3] LLM-KD: Gu et al. 2023 https://arxiv.org/abs/2306.08543
[P1] LLM-Pruner: Ma et al. 2023 https://arxiv.org/abs/2305.11627
[P2] Optimal BERT Surgeon: Kurtic et al. 2022 https://arxiv.org/abs/2203.07259
[P3] What Matters in Structured Pruning: Santacroce et al. 2023 https://arxiv.org/abs/2302.03773
[P4] RigL: Evci et al. 2020 https://arxiv.org/abs/2005.07233
[L2] QLoRA: Dettmers et al. 2023 https://arxiv.org/abs/2305.14314
[L3] Adapters: Houlsby et al. 2019 https://proceedings.mlr.press/v97/houlsby19a.html
Thank You for Reading!
Laith Zumot © 2025 · lzumot.github.io · CC BY-NC-SA 4.0